转自：

1、稀疏：什么是K稀疏呢?

在压缩感知里经常提到 “K稀疏” 的概念，这个是很容易理解的：也就是对于长度为N的向量（实际上是指一个N维离散离值信号）来说，它的N个元素值只有K个是非零的，其中K<<N，这时我们称这个向量是K稀疏的或者说是严格K稀疏的；实际中要做到严格K稀疏不容易，一般来说，只要除了这K个值其它的值很小很小，我们就认为向量是稀疏的，这时区别于严格K稀疏且就叫它K稀疏吧。

为什么要谈稀疏这个问题呢？因为如果信号是稀疏的，则它是可压缩的，也就是说里面那么多零，我只记录那些非零值及它的位置就好了。

当然，现实中的信号本身一般并不是稀疏的，但经过一个变换后，在一组基上面是稀疏的，这就是信号的稀疏表示。

稀疏性是压缩感知的前提。

2、范数||x||p

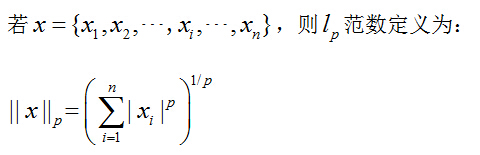
常见的有l0范数、l1范数、l2范数，经常要将l0范数等价为l1范数去求解，因为l1范数求解是一个凸优化问题，而l0范数求解是一个NP难问题，这些后面慢慢再说。

l0范数指的是x中非零元素的个数，即x的稀疏度，如果x是K稀疏的，则l0范数等于K；

l1范数指的是x中所有元素模值的和

l2范数指的是x中所有元素模值平方的和 再开方，这个带公式就可以了，它代表着距离的概念

还有无穷范数，指的是x中元素模的最大值

3、符号arg min

压缩感知中常见如下表示：

 

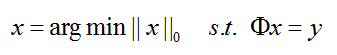
s.t. 表示 受约束于，是“subject to”的缩写。

为了说明argmin的含义，可以参见Wikipedia中对的解释：

argmax : In , arg max stands for the argument of the maximum, that is to say, the set of points of the given  for which the given  attains its  .

（即求当满足约束条件时，使函数达到最大值的x）

 

举三个例子自己体会一下就可以了：

 

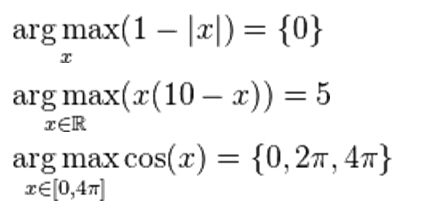
argmin与其类似，琢磨一下就是了。

下面转一段话：（）

y = f(t) 是一般常见的函数式，如果給定一个t值，f（t）函数式会赋一个值給y。

y = max f(t) 代表：y 是f(t)函式所有的值中最大的output。

y = arg max f(t) 代表：y 是f(t)函式中，会产生最大output的那个参数t。

看起来很模糊，举个例子应该比较好理解：

假设有一个函式 f(t)，t 的可能范围是 {0,1,2}，f(t=0) = 10 ; f(t=1) = 20 ; f(t=2) = 7，那分別对应的y如下：

y = max f(t) = 20

y= arg max f(t) = 1

 

这一块要好好说一说，因为这是压缩感知最基本的表示，是最常见的，但在不同的论文里面表示是不统一的：

a)焦李成，杨淑媛，刘芳，侯彪.压缩感知回顾与展望[J].电子学报，2011，39(7)：1651-1662.

b)石光明，刘丹华，高大化，刘哲，林杰，王良君.压缩感知理论及其进展[J].电子学报，2009，37(5)：1070-1081.

 

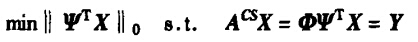
c)杨海蓉，张成，丁大为，韦穗.压缩传感理论与重构[J].电子学报，2011，39(1)：142-148.

 

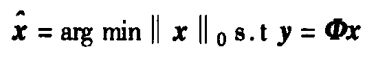
在压缩感知理论方面，不管是用min还是argmin（文献ab与文献c区别），不管min下面有没有变量（文献a与文献b区别），其实表达的意思都是一样的：

如果用0范数，则是求得满足后面约束条件的最稀疏的x(或θ)；

如果用1范数，则是求得满足后面约束条件的元素模值和最小的x(或θ)；

 

当然两种求法在满足一定条件下(RIP)是等价的，RIP又是另一回事了，慢慢以后再说吧。